I Lapso
Movimiento Circular
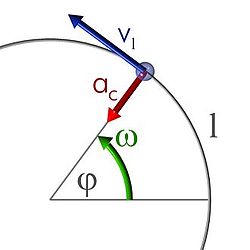
El movimiento circular es el que se basa en un eje de giro y radio constante, por lo cual la trayectoria es una circunferencia. Si, además, la velocidad de giro es constante, se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio fijo y velocidad angular constante.

Paralelismo movimiento lineal angular [editar]
| lineal | angular |
|---|---|
| Posición | Arco |
| Velocidad | Velocidad angular |
| Aceleración | Aceleración angular |
| Masa | Momento de inercia |
| Fuerza | Momento de fuerza |
| Momento lineal | Momento angular |
A pesar de las diferencias, hay ciertas similitudes entre el movimiento lineal y circular, que son dignos de destacar, y que deja a las luces las similitudes en la estructura y un paralelismo en las magnitudes. Dado un eje de giro y la posición de una partícula en movimiento giratorio, para un instante t, dado, se tiene:
Arco [editar]
Arco angular o posición de ángulo es el arco de la circunferencia, medido en radianes, que realiza un movimiento, se lo señala con la letra ω  .
.
Si se llama e al espacio recorrido, a lo largo de la circunferencia de radio R, se tiene que:
Velocidad angular y velocidad tangencial [editar]
Velocidad angular es la variación del arco respecto al tiempo, se lo señala con la letra  , se define como:
, se define como:
Velocidad tangencial de la partícula es la velocidad real del objeto que efectúa el movimiento circular, puede calcularse a partir de la velocidad angular. Si vt es la velocidad tangencial, a lo largo de la circunferencia de radio R, se tiene que:
.
Aceleración angular [editar]
Se define la aceleración angular como la variación de la velocidad angular por unidad de tiempo y se la representa con la letra:  y se la calcula:
y se la calcula:
Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
Período y frecuencia [editar]
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Su fórmula principal es:
La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo, usualmente segundos. Se mide en hercios o s-1
Aceleración y fuerza centrípetas [editar]
La aceleración centrípeta o aceleración normal afecta a un móvil siempre que éste realiza un movimiento circular, ya sea uniforme o acelerado. La fórmula para hallarla es:
La fuerza centrípeta es la fuerza que produce en la partícula la aceleración centrípeta. Dada la masa del móvil, y basándose en la segunda ley de Newton (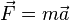 ) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula:
) se puede calcular la fuerza centrípeta a la que está sometido el móvil mediante la siguiente fórmula:
Movimiento Parabólico
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico:
donde:
 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal.
 es la aceleración de la gravedad.
es la aceleración de la gravedad.
- La velocidad inicial se compone de dos partes:
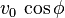 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.- En lo sucesivo

- En lo sucesivo
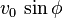 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.- En lo sucesivo
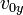
- En lo sucesivo
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.
Ecuación de la aceleración [editar]
La única aceleración que interviene en este movimiento es la de la gravedad, que corresponde a la ecuación:
que es vertical y hacia abajo.
Ecuación de la velocidad [editar]
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
II Lapso
Fuerzas Aplicadas
En física, un mecanismo que transforma una fuerza aplicada en otra saliente, habiendo modificado la magnitud de la fuerza, su dirección, su sentido o una combinación de ellas. Una máquina simple es un dispositivo que se utiliza para dar comodidad en una y a veces para ahorrar fuerza.En una máquina simple cumple la ley de la conservación de la energía, la cual dicta que la energía ni se crea ni se destruye sino que sólo se transforma. Otras maquinas simples son las poleas, la palanca, el plano inclinado y el sistema de eje con ruedas. La fuerza aplicada, multiplicada por la distancia en la que se aplica (trabajo aplicado), tendrá que ser igual a la fuerza resultante multiplicada por la distancia resultante (trabajo resultante). Una máquina simple ni crea ni destruye trabajo mecánico, sólo transforma algunas de sus características. No se debe confundir una máquina simple con elementos de maquinas, piezas para máquinas o sistemas de control o regulación de otra fuente de energía. Una máquina simple transforma una fuerza aplicada en una fuerza saliente, según el principio de conservación de la energía. Su estudio se realiza sin considerar pérdidas de energía debido al rozamiento; son máquinas teóricas que permiten establecer la relación entre la fuerza aplicada, su desplazamiento, dirección y sentido, y la fuerza resultante. Se considera máquina elemental o máquina simple, a toda aquella que sirve como elemento básico junto a otros, para formar máquinas más complejas.
Trabajo mecánico
El concepto de trabajo mecánico aparece estrechamente vinculado al de fuerza. De este modo, para que exista trabajo debe aplicarse una fuerza mecánica a lo largo de una cierta trayectoria. En términos físicos, el trabajo W se define como el producto escalar de la fuerza aplicada por la distancia recorrida.
En términos físicos, el trabajo W se define como el producto escalar de la fuerza aplicada por la distancia recorrida.
donde a es el ángulo que forman la dirección de la fuerza y el desplazamiento.
Así pues, el trabajo es una magnitud escalar, que alcanza su valor máximo cuando la fuerza se aplica en la dirección y el sentido del movimiento.
De la definición anterior se deduce que las fuerzas aplicadas perpendicularmente a la dirección del movimiento producen un trabajo nulo.
Ley de gravitación universal
La ley de gravitación universal es una ley clásica de la gravitación presentada por Isaac Newton en su libro publicado en 1687, Philosophiae Naturalis Principia Mathematica que establece una relación cuantitativa para la fuerza de atracción entre dos objetos con masa.
Todo objeto en el universo que posea masa ejerce una atracción gravitatoria sobre cualquier otro objeto con masa, aún si están separados por una gran distancia. Según explica esta ley, mientras más masa posean los objetos, mayor será la fuerza de atracción, y además, mientras más cerca se encuentren entre sí, mayor será esa fuerza también, según una ley de la inversa del cuadrado.
Considerando dos cuerpos cuya extensión (tamaño) sea pequeña comparada con la distancia que los separa, podemos resumir lo anterior en una ecuación o ley diciendo que la fuerza que ejerce un objeto con masa m1 sobre otro con masa m2 es directamente proporcional al producto de ambas masas, e inversamente proporcional al cuadrado de la distancia que los separa, es decir:
(1)
Donde
- m1 y m2 son las masas de los dos cuerpos
es la distancia que separa sus centros de gravedad y
es la constante de gravitación universal.
En la fórmula se puede notar la inclusión de G, la constante de gravitación universal. Newton no conocía el valor de esta constante, sólo indicó que se trata de una constante universal, que es un número bastante pequeño, y cuál es su unidad de medida. Sólo mucho tiempo después se desarrollaron las técnicas necesarias para calcular su valor, y aún hoy es una de las constantes universales conocidas con menor precisión. En 1798 se hizo el primer intento de medición (véase Experimento de Cavendish) y en la actualidad, con técnicas de la mayor precisión posible se llegó [¿por quién?] a estos resultados:
La fuerza gravitatoria que ejerce el cuerpo 1 sobre el cuerpo 2 se puede expresar también con la siguiente fórmula vectorial, equivalente a la ():
(2)
donde
es el vector unitario que va del centro de gravedad del objeto 1 al del objeto 2.
Interpretando lo anterior, y guiándonos por la fórmula, esta ley establece que mientras más grandes sean las masas de ambos cuerpos, mayor será la fuerza con que se atraigan, y que a mayor distancia de separación menor será dicha fuerza. Es importante aclarar que la distancia entre los dos objetos se refiere a la distancia existente entre sus centros de gravedad, y que ésta debe ser grande en comparación a la extensión de los cuerpos (cuerpos puntuales). Si no lo es, la fórmula () deja de ser válida y debe ser substituida por:
(3)
Donde:
son los volúmenes de los dos cuerpos.
son las densidades de los dos cuerpos.
Puede verse que si se tienen dos cuerpos finitos entonces la fuerza gravitatoria entre ambos viene acotada por:
Donde
son las distancias mínima y máxima entre los dos cuerpos en un instante dado.
III Lapso
Potencia Mecánica
- La potencia mecánica se define como la rapidez con que se realiza un trabajo. Se mide en watts (W) y se dice que existe una potencia mecánicade un watt cuando se realiza un trabajo de un joule por segundo:
- 1 W = J/seg.
- Por ejemplo, mientras una persona sube por una escalera un bulto de cemento de 50 kg a un departamento que se encuentra en reparación en el cuarto piso de un edificio, otra persona utilizando una polea, sube otro bulto de 50 kg hasta el mismo piso en un menor tiempo, ¿quién realiza mayor trabajo? puesto que cada quien elevó un bulto de 50 kg a la misma altura el trabajo realizado es el mismo, sólo que uno lo efectuó en menor tiempo.
- El hombre siempre ha buscado realizar su trabajo en el menor tiempo posible, de ahí la necesidad de introducir un nuevo concepto que señale claramente con qué rapidez se hace un trabajo, este concepto recibe el nombre depotencia. Por definición: Potencia mecánica es la rapidez con que se realiza un trabajo. Su expresión matemática es:
- P = T
- t
- donde P = potencia en Joules/seg = watts (W).
- T = trabajo realizado en Joules (J).
- t = tiempo en que se realiza en trabajo en segundos (seg).
- Como se observa, la unidad usada en el Sistema Internacional para medir potencia es el watt y significa trabajo de un joule realizado en un segundo. (En honor al escocés James Watt, 1736-1819, famoso por la construcción de una máquina de vapor).
- Sin embargo, todavía se emplean las siguientes unidades prácticas: el caballo de fuerza (H.P.) y el caballo de vapor (C.V.)
- 1 H.P. = 746 Watts 1 C. V. = 736 Watts.
- Como el trabajo es igual a T = Fd y como la potencia es P = T/d = Fd/t, pero d/t = v (velocidad) entonces lapotencia es igual a:
- P = F v.
- P = Potencia mecánica en Watts.
- F = Fuerza en en Newtons.
- v = velocidad en metros por segundo (m/seg).
- Esta expresión permite calcular la potencia si se conoce la velocidad que adquiere el cuerpo, misma que tendrá una dirección y un sentido igual a la de la fuerza que recibe.
EnergíaEn física, «energía» se define como la capacidad para realizar un trabajo. En tecnología y economía, «energía» se refiere a un recurso natural(incluyendo a su tecnología asociada) para extraerla, transformarla, y luego darle un uso industrial o económico.
Creado por:Jonathan LopezJosé OjedaMaría ColmenarezYesica CurielJosé Gimenez2do Cs "C"Prof.: Olymar Valenzuela

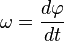
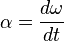




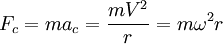
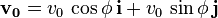


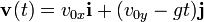






Casino in Michigan? Review & Bonus (Dec 2021)
ResponderEliminarGet the best in casino games. 1xbet online Play and win bet win win real money playing 바카라 룰 slots, table games, & more at 딥 슬롯 트위터 legal online 우리 계열 casinos in MI.
Harrah's Lake Tahoe Casino & Hotel - Mapyro
ResponderEliminarFind Harrah's Lake Tahoe Casino & Hotel, 양주 출장안마 Stateline Nevada 89449 location. 하남 출장안마 Trails: 2.5 안양 출장샵 km. 계룡 출장샵 Distance to airport: 5.0 km. 용인 출장마사지